População e amostra - Professora Noemi Matemática

Estatística Descritiva: População, Amostra e Amostragem

O que é Estatística?

A Estatística é uma parte da Matemática que fornece métodos para coleta, organização, descrição, análise e interpretação de dados. A estatística é dividida em duas partes: descritiva e inferencial. Nesse post vou explicar o que é estatística descritiva, população, amostra e amostragem.

Estatística Descritiva
A Estatística Descritiva fornece um conjunto de técnicas destinadas para descrever e resumir dados, a fim de que possamos tirar conclusões a respeito de características de interesse.
Utilizamos a Estatística Descritiva quando tomamos contato com os dados pela primeira vez, os dados são exibidos de forma resumida e utilizamos tabelas e gráficos para representar o conjunto de dados.

Estatística inferencial
Estatística inferencial é o estudo de técnicas que possibilitam a extrapolação das informações e conclusões obtidas a partir de subconjuntos de valores, geralmente de dimensões menores. O uso das técnicas é indispensável quando existe a impossibilidade de acesso a todo o conjunto de dados, com isso, fazemos uma generalização com base no que foi coletado na estatística descritiva.

População, amostra e amostragem

População

Em estatística quando falamos população nós estamos nos referindo a população estatística. Podemos definir de forma muito simples que população são as pessoas, objetos e eventos de interesse de estudos.

Exemplos:
1. Alunos matriculados nas escolas públicas no ano de 2022;
2. Todas as pessoas que compraram celular na região Sudeste do Brasil.

Amostra

Supondo que precisamos fazer uma pesquisa sobre a intenção de votos nas próximas eleições. Nesse exemplo nossa população estatística são os eleitores brasileiros, ou seja, todos brasileiros que podem votar.
Devido a impossibilidade de fazer a pesquisa com todos os eleitores (que é nossa população) nós “retiramos” uma parte dessa população que chamamos de amostra. Os estudos serão realizados na amostra, portanto, a amostra precisa ter as mesmas características da população, isso é tem grande importância.
O processo de escolha da amostra é chamado de amostragem e existem técnicas de amostragem.

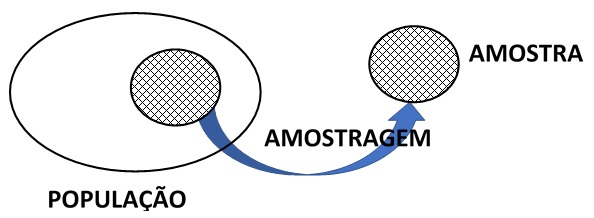
POPULAÇÃO – indivíduos ou objetos que apresentam pelo menos uma característica em comum.
AMOSTRA – subconjunto finito da população
AMOSTRAGEM – técnica utilizada para recolher amostras.

Amostragem

As técnicas de amostragem estão divididas em dois grandes grupos: amostragem probabilística e amostragem não probabilística.

· Na amostragem não probabilista os elementos têm chances (no sentido de probabilidade) diferentes de serem escolhidos.

· Na amostragem probabilística todos elementos tem a mesma chance (a mesma probabilidade) de serem escolhidos.

A seguir vou demonstrar as principais técnicas de amostragem probabilística.

Amostragem casual ou aleatória simples

Todos os elementos da amostra devem ter a mesma chance (probabilidade) de serem escolhido (equivalente a um sorteio de BINGO).

Exemplo
Uma professora escreve o nome de todos os seus alunos em pedaços de papel (supondo que a turma tenha 40 alunos) e coloca em um saquinho. Depois de misturá-los, sorteia 10 nomes.

Amostragem proporcional estratificada

Utilizada quando a população se divide em subpopulações, subgrupos, chamadas de estratos.
É provável que a variável em estudo apresente comportamentos distintos dentro de cada estrato.
Os elementos da amostra devem levar em consideração tais estratos e também ser proporcional ao número de elementos dos estratos.

Exemplos
1) Imaginem que temos que realizar uma pesquisa numa escola. A população da escola está dividida em 3 subpopulações: 70% são alunos, 20% são colaboradores e 10% são professores, dividida em 3 estratos.

Para retirarmos a amostra temos que manter a proporcionalidade dos estratos, ou seja, a amostra que será um subgrupo da população precisa ter 70% alunos, 20% colaboradores e 10% professores.

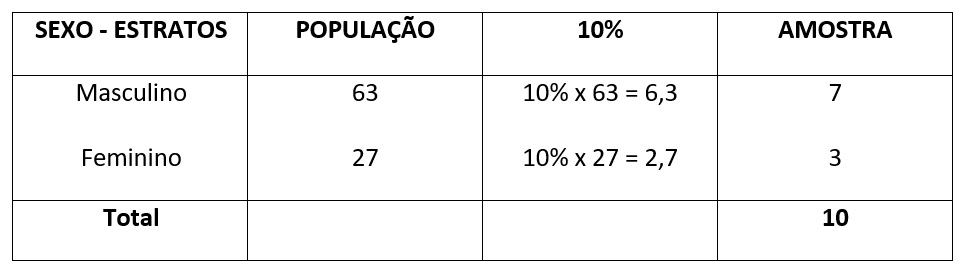
2) Uma empresa possui 63 homens e 27 mulheres perfazendo um total de 90 funcionários. Obtenha a amostra proporcional estratificada de 10% da população.

Observe que a população está dividida em 2 estratos: masculino e feminino.
Temos que retirar uma amostra de 10% dessa população, mas manter a proporcionalidade.

Homens: 10% de 63 = 6,3 aplica as técnicas de arredondamento, teremos 7 homens.
Mulheres 10% de 27 = 2,7 aplica as técnicas de arredondamento, teremos 3 mulheres.
Total da amostra = 10 pessoas

Estatística Descritiva: População Amostra

Exercício
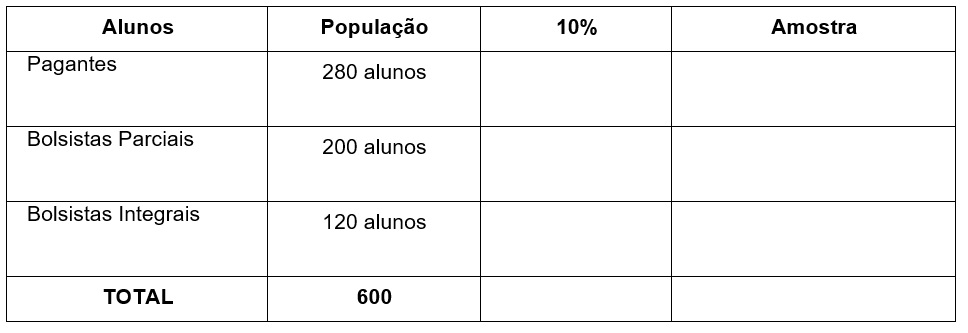
O diretor de uma escola, na qual estão matriculados 600 alunos, sendo: 280 alunos pagantes, 200 alunos bolsistas parciais e 120 alunos bolsistas integrais, têm interesse em conhecer as condições de vida extraescolar de seus alunos, e não dispondo de tempo para entrevistar todas as famílias, resolveu fazer um levantamento por amostragem em 10% dessa população. Quantos alunos pagantes, bolsistas parciais e bolsistas integrais, respectivamente, devem ser entrevistados?

Para conferir a resposta assista o vídeo nesse link, minuto 7.

Download do Material

Amostragem Sistemática

Esta técnica pode ser utilizada quando a população já se encontra ordenada.
Exemplo: prontuários médicos, cadastro de funcionários, cadastro de clientes, matrícula de alunos.

Exemplo
Num hospital particular de uma determinada cidade há 20 estagiários de enfermagem. A nutricionista do hospital tem interesse em conhecer os hábitos alimentares desses estagiários, e não dispondo de tempo para entrevistar todos, resolveu fazer um levantamento com 5 estagiários.
Os dados cadastrais estão organizados em prontuários numerado de 1 a 20.
Obtenha uma amostra sistemática de tamanho igual a 5.

Resposta:

Lembrando, para aplicar essa técnica os dados precisam estar organizados.
Temos: POPULAÇÃO = 20 estagiários AMOSTRA = 5 estagiários

Utilize a fórmula:

O que significa esse número 4 que encontramos?
Ele vai nos auxiliar em dois momentos:
1º) obter o 1º elemento da amostra
2º) ele determina o passo
Para obter o 1º elemento da amostra, ou seja, a 1ª ficha, realize um sorteio tipo bingo das fichas de 1 até 4. Faz de conta que sorteamos a ficha número 2, então nossa primeira ficha é a de número 2.
Agora vamos andar 4 passos para encontrar as próximas fichas.

2 + 4 (passos) = 6 à a segunda ficha será a número 6
6 + 4 (passo) = 10 à a terceira ficha será a número 10
10 + 4 (passo) = 14 à a quarta ficha será a número 14

14 + 4 (passo) = 18 à a quinta ficha será a número 18

Exercício: População, Amostra, Amostragem

Dessa forma encontramos os alunos que participarão da entrevista junto à nutricionista, são os alunos das fichas números 2, 6, 10, 14 e 18.

Abaixo faço um resumo dos assuntos que foram abordados nesse post e espero que tenha auxiliado de alguma forma.

– O que é Estatística
– Estatística Descritiva
– Estatística Inferencial
– O que é População em Estatística
– População e Amostra
– Qual a diferença entre população e amostra
– Como calcular a amostra em uma população
– População e Amostra Exercícios

– Amostragem
·         Amostragem Probabilista
·         Amostragem não probabilística

– Tipos de Amostragem:
1)      Amostragem casual ou aleatória simples – também conhecida como amostra aleatória simples
2)      Amostragem proporcional estratificada – também conhecida como amostra estratificada
3)      Amostragem sistemática – também conhecida como amostra sistemática
Amostragem Exercícios

Para ter acesso as mesmas informações, mas em vídeo, acesse o link a seguir clique aqui.